概念
首先介绍一下 有限自动机 FA (Finite Automate)的概念,形式上它是一个五元组 \( (S, \sum, \delta, s_0, S_A) \)
- \( S \) 是识别器的有限状态集,以及一个错误状态\( S_e\)
- \( \sum \)是识别器使用的有限字母表。通常,\( \sum \) 是转移图中边的标签合集
- \( \delta(s, c) \)是识别器的转移函数。它将每个状态 \(s \in S \)和每个字符\(c \in \sum \)映射到下一个状态。在状态\( s_i \)遇到输入字符\(c\),FA将采取\(s_i \rightarrow^c \delta(s_i, c)\)
- \(s_0 \in S\) 是制定的起始状态
- \( S_A \) 是接受状态的集合,\(S_A \subseteq S\),通常在转移表中为双层圆圈
NFA是不确定有穷自动机(Nondeterministic Finite Automata)
DFA是确定有穷自动机(deterministic finite automaton )
正则表达式
这三者是等价的,本文要讲的是NFA -> DFA的转化
区别
NFA和DFA最大的区别就是NFA允许输入\( \epsilon \)进行转移,其状态对同一字符输入有可能多种转移
子集构造
1.DFA的状态集
首先先定义几个概念
edge
\(edge(s, c)\)表示从状态\(s\)沿着字符c可以到达的所有NFA状态的集合closoure(闭包)
对于状态集合\( S \),\( clousre(S)\)是从\(S\)状态触发,无需接受任何字符,只沿\( \epsilon \)边就可以到达的状态组成的集合。求闭包的算法如下
$$
\begin{matrix}
T \leftarrow S \\
repeat & T^{'} \leftarrow T \\
& T \leftarrow T^{'} \cup (\cup_{s \in T^{'}}edge(s, \epsilon )) \tag{公式1} \\
until & T = T^{'}\\
\end{matrix}
$$
依据这个我们就可以构造出对应DFA的状态集:
对于NFA某个状态集合d出发,输入c,所能到达的状态集合并记为\( DFAedge(d, c)\),具体表达式如下:
$$ DFAedge(d, c) = closure(\cup_{s \in d}edge(s, c)) \tag{公式2} $$
这里是通过原有的NFA一些状态集构造新的DFA状态的算法过程
真实NFA -> DFA的 构造过程的算法公式比较繁琐,但跟数学归纳法类似,直接通过下面例子说明
2.起始项
上面部分讲的是中间递推过程,例子里面需要的是起始项
也就是DFA的起始状态,设为\( DFA\_s_0 \),记NFA的起始状态为\( NFA\_s_0 \),那么
$$ DFA\_s_0 = closure( NFA \_s_0 ) \tag{公式3} $$
3.例子
拿装配脑袋的文章例子说明
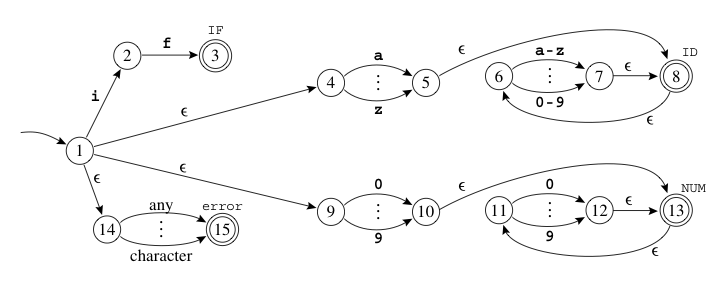
起始项
\( NFA \_s_0 = { S_{[1]} } \)
\( DFA\_s_0 = closure( NFA \_s_0 ) = closure({ S_{[1]} } ) \)
由于\( edge(S_{[1]}, \epsilon ) = \{S_{[1]} , S_{[4]}, S_{[9]}, S_{[14]} \}\)
满足 公式1中 \( T = T^{'} \),故而\( DFA\_s_0 = \{S_{[1]} , S_{[4]}, S_{[9]}, S_{[14]} \} \)
递推过程
对于状态
\( DFA\_s_0 = \{S_{[1]} , S_{[4]}, S_{[9]}, S_{[14]} \} \),如何求出另一个转移函数和状态
就从转移字符i来说,看公式2
此时有\( d = \{S_{[1]} , S_{[4]}, S_{[9]}, S_{[14]} \}, c = 'i' \)
那么 \( \cup_{s \in d}edge(s, c) = \{ S_{[2]}, S_{[5]}, S_{[15]}\} \),继续求\( closure(\{S_{[2]}, S_{[5]}, S_{[15]}\}) = \{ S_{[2]}, S_{[5]}, S_{[15]}, S_{[8]}, S_{[6]} \} \)
所以新的DFA的\( \delta(DFA\_s_{0}, 'i') = \{ S_{[2]}, S_{[5]}, S_{[15]}, S_{[8]}, S_{[6]} \} \)
如下图
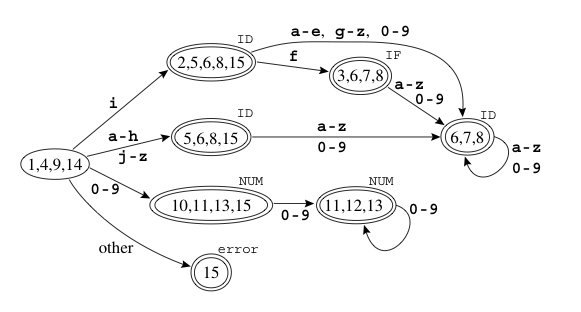
其他
公式2 支持分配律\( DFAedge(d, c) = closure(\cup_{s \in d}edge(s, c)) = \cup_{s \in d}(closure(edge(s, c))) \)