用法
泵定理(pumping lemma):判断一个语言不是正则语言,通常使用反证法(泵引理是RL语言的必要条件)
原理
设\( L \) 是一个RL,则存在仅依赖于\( L \)的正整数\( P \)
对于\( \forall w \in L \), 如果\( |w| \ge P \),则存在\( x, y, z \in \Sigma^{*} \) 满足\( w = xyz \),同时有:
(1) \( |xy| \le P \)
(2) \( |y| \ge 1\)
(3) \( \forall i \in N^{0},xy^{i}z \in L\)
上叙是自然语言,用正式表达式 (formal expression)如下
$$\begin{align}
(\forall L & \subseteq \Sigma^{*}) \\
& (regular(L) \Rightarrow \\
& ((\exists P \ge 1)((\forall w \in L)((|w| \ge P) \Rightarrow \\
& ((\exists x, y, z \in \Sigma^{*})(w = xyz \land (|xy| \le P \land |y| \ge 1 \land (\forall i \in N^{0})(xy^{i}z \in L))))))))
\end{align}$$
图形结合
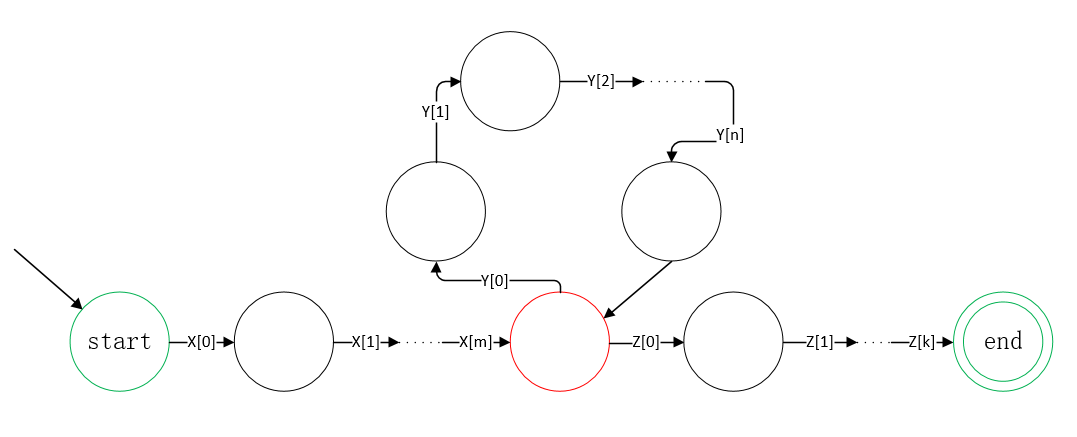
所以对于y这个字符串来说,无论中间重复多少遍,都是会回到红色的状态中
其中P可以取值 = 最小DFA状态数
证明
试证明上下文无关文法\(L = \{0^{n}1^{n} | n \ge 1\} \)不是RL
反证法:设\(L = \{0^{n}1^{n} | n \ge 1\} \)是RL,则\( L \)满足泵引理. 不妨设 \( P \)是仅依赖于 \( L \)的正整数
取语句\( w = 0^{P}1^{P}\),由\( L \)的定义可知 \( w \in L\).
此时\( |w| = 2P \ge P \),由定理结论
(1) \( |xy| \le P\)
(2) \( |y| \ge 1\)
可知 \( x、y \)一定是形如 \(x = 0^g(g \ge 1) , y = 0^h(h \ge 1)\)
那么倒推出 \(z = 0^{P-g-h}1^P \)
取定理结论(3)中变量\(i = 2\),则\( xy^2z = 0^g (0^h)^2 0^{P-g-h}1^P = 0^{P+h}1^P \notin L\),不满足定理结论(3),得出矛盾
假设不成立,得证
实际上,正则语言不具有计数性.
例如编译原理中,利用正则表达式(DFA、NFA)做完词法分析,需要引入更强的语法 上下文无关文法 去做语法分析